免费qq黄钻网站大全下载 boost之王牌Xgboost

找寻了好多blog发觉，对于xgboost多数只是径直陷入公式推导，而xgboost究竟是什么却压根未能讲明白讲透彻，处于仅仅知晓个大概，了解似是而非的状况。撰写一篇blog将其总结一番嘻嘻。

Xgboost

首先得讲明白，Xgboost乃是由好些个CART所构成的回归树 ，这个务必得明确呀，Adaboost属于分类提升，而Xgboost是回归提升 ！

那么，分类树也就是决策树，跟回归树的区别是什么呢？通俗来讲，决策树依据特征信息所得到的是标签，而回归树得到的是一个值，我们能够认为这个值是这个特征组合的权重值。那么，对于回归树而言，肯定无法借助信息增益、Gini系数这些方法来判定是否分裂。那么，回归树怎样判断分裂效果呢？当然是拟合得越接近越好，也就是说，可以采取均方误差或者指数误差来作为评价标准。

这个时候，大家能够感受到，一个回归树形成的关键点在于，其一，分裂点依据什么进行划分，比如前面所说的均方误差最小，loss；其二，分类后的节点预测值是多少，比如前面所讲，有一种情况是将叶子节点下各样本实际值的均值作为叶子节点预测误差，或者通过计算得出。

涉及提升这方面，前面的blog有提及，这是当然的，Xgboost是通过多个弱学习器组合在一起的，是将这些相加从而形成一个强学习器，那么针对Xgboost来讲，首先要明确我们的目标，我们期望去建立K个回归树，目的是让树群的预测值能够尽可能地贴近真实值，同时具备尽可能大的泛化能力，还需要考虑之前我们所定义的提升的目标函数，。

其中，l是损失函数，我们期望将第t个学习器学习到的数值进行集成而后得到的预测值，与真实值之间的误差越小越棒。 其次，后面的函数是正则化，用于表示第t棵树的复杂度，当然的是，复杂度越小意味着树的泛化能力越出色。

就直观的角度去看，目标提出的要求是，要让预测的误差尽可能地小，要让叶子结点可以尽最大可能少，还有要让节点的数值尽可能不会处于极端的状态（而过拟合所存在的风险又该如何考量呢），如此一来，便又回到最开始的那个问题了，也就是怎样去选择回归树的分裂点呢，那么对于这个节点的预测数值应该怎样去进行表达呢，难道是要采用取平均这种显得不上档次的办法吗。嘻嘻嘻，Xgboost所采用的做法乃是贪心策略加上最优化（二次函数所处最佳状态的那种最优化），随之便分开来对这两个核心要点进行介绍 。

输出预测值最优化推导

在此处，我们首要针对回归树的形式以及树的复杂度予以定义，将树f(x)拆解为结构部分q与叶子回归值w。下面这张图是一个具体的例子。结构函数q把输入映照到叶子的索引号之上，而w给出了每个索引号对应的叶子分数是多少。

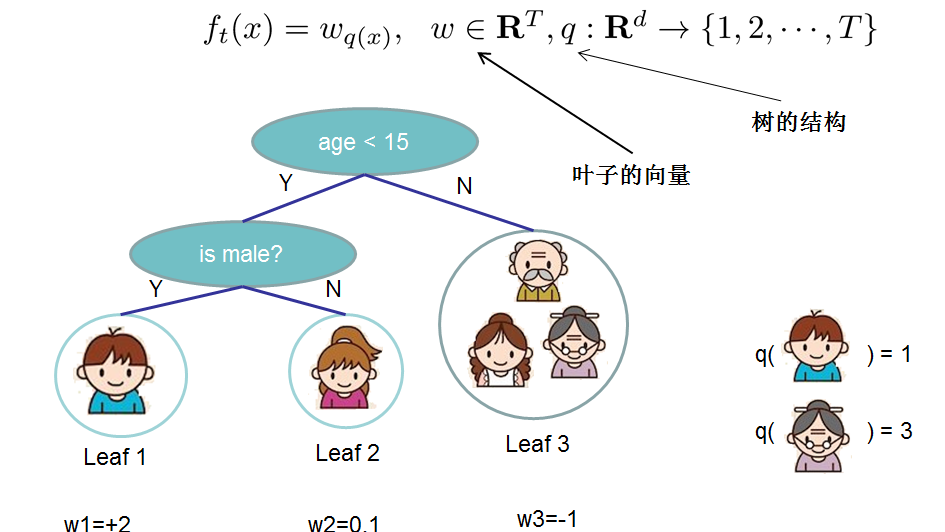
对树而言，其复杂度涵盖了叶子结点的数量，以及针对输出回归值的约束形式，下图存在一个具体的示例 。

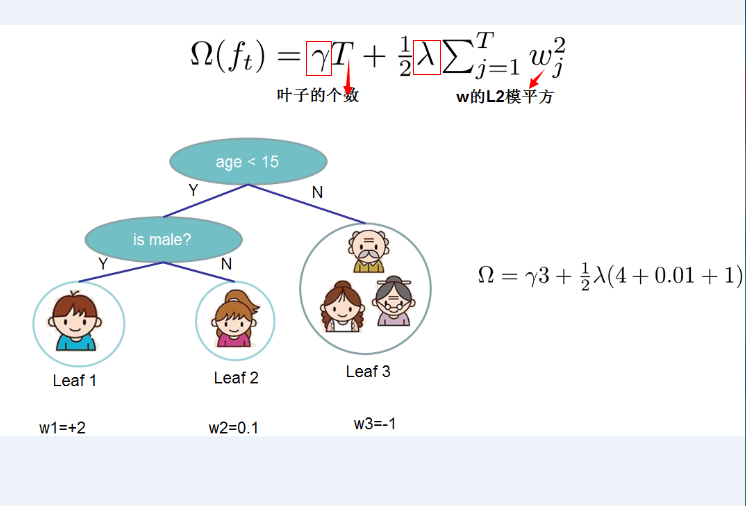
完成这两部分定义后，我们再来审视目标函数，我们曾提及借助最优化的途径去求解，那么，我们针对目标函数运用泰勒公式进行二次展开，进而得出如下形式：

在有了上面针对 f（x）以及复杂度进行定义以后，我们能够对目标函数展开改写，并且其中 I 被界定为处于每个叶子之上的样本集合，句号。

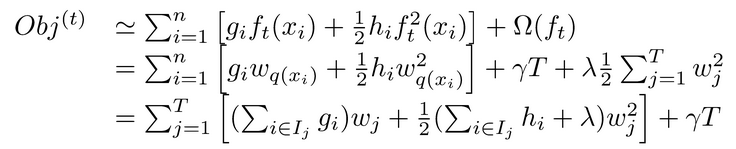
（ps：担心小白不明白，之所以能够这样改写，是因为不管是决策树还是回归树，一旦被划分到相同的特征空间之后，输出的值都是相同的，所以我们能够只考虑叶子节点的权值，有多少个样本属于这个叶子结点，那么原始的值在叶子结点上相应加上多少个就可以了。）。

随便大致瞧一眼，这难道不就是二次函数进行最优化的情况嘛！仅仅需要求得让一阶导数等于0的那个点，。

值就得到了难道不是loss的最小值吗！在这样的情形之下，我们把Gj，Hj定义成为如下的格式：

最终目标函数可以化简为：

通过对

求导等于0，可以得到

然后把

最优解代入得到：

经由这种方式，我们便获取到了回归树叶子结点的输出值，这同样是Xgboost的创新点中的一个赏金女王pg破解版下载，缘由在于我们能够自行定义目标函数，因为taylor展开式助力我们能够使任意形式的函数全部露出本来的样子，其最终都能够转化为二次函数最优化的形式，。

节点分裂策略（贪心策略）

这里运用贪心策略是怎样的情况呢，起初你拥有一群样本，将其放置于第一个节点之时，此刻T等于1，那么w是多少呢，并不知晓，它是通过计算得出的，处于这个时候，所有样本的预测值均为w（在此处需自行深入领会，决策树的节点显示类别，回归树的节点呈现预测值），把样本的label数值代入进去，从而得到了T等于1时的loss function。后面陆续进行，紧接着挑选一个特征分裂成两个节点，使之成为一棵弱小的树苗，这种情况下需求如下：（1）明确用于分裂的特征，具体怎么做？最为简单的是采用粗暴的枚举方式，挑选损失函数效果最为理想的那个（关乎此粗暴枚举，Xgboost的改良并行方式我们稍后研读）；（2）以何种方式确立节点的权重以及最小的损失函数，这在我们上一步已然解决 。

那么节奏是，先选择一个feature进行分裂，接着计算loss function的最小值，此后再选一个feature分裂，又一次得到一个loss function最小值，如此这般，你将其全部枚举完，从中找一个效果最好的www.pg.qq.com，进而把树给分裂，最终就得到了小树苗。

当处于分裂状态时，你能够留意到，每当节点进行分裂之际，唯有归属于该节点的那些样本才会对损失函数造成影响，所以每次实施分裂时，要去计算分裂所带来的增益（也就是损失函数的降低幅度），仅仅需要聚焦于打算进行分裂的那个节点所涵盖的样本即可。具体的公式如下：

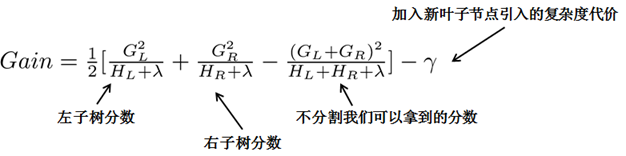
之后，持续分裂，依据上文提到的那种方式，构建出一棵树，又构建出一棵树，每一回都在上一回的预测基础之上选取最优的情况进而进一步分裂、建树，这难道不是贪心策略吗？

凡是这种循环迭代的方式必定有停止条件，什么时候停止呢：

（1）当引入的那个分裂所带来的增益小于某一个阀值之际，我们能够剪掉这个分裂，所以并非每一回分裂，loss function整体都会出现增加的情况，这有点类似预剪枝的概念，（实际上我在这儿是存有疑问的，通常后剪枝的效果会比预剪枝更好一些吧，只是会更复杂麻烦些，在此还望大神予以指教，为何此处运用的是预剪枝的思想，当然Xgboost是支持后剪枝的），阈值参数是γγ，正则项里叶子节点数T的系数，（大神请予以确认）；。

（2）树达到最大深度之际，便停止建立决策树，设置一个超参数max_depth，这挺好理解的，树要是太深，非常容易出现学习局部样本的状况，进而过拟合，。

当样本权重和小于设定阈值时，就会停止建树，对此进行解释一下，这里涉及到一个超参数，就是最小的样本权重和-min_child_weight，它和GBM的min_child_leaf参数类似，然而又不完全一样，其大意是，要是一个叶子节点的样本数量太少了，那么同样会终止，这也是过拟合的情况；。

总结

w，它是通过最优化的方式被求出来的，并非是借助什么平均值或者规则来指定的，这样的情况，算得上是在思路方面具备一定新颖性的吧；。

正则化这项用于防止过拟合的技术，上述已然看到，它直接就在loss function里面存在着 。

可以支持进行自定义的loss function，哈哈，我就不多说了，只要是能够进行泰勒展开的（也就是能求一阶导数以及二阶导数的）就可以，你觉得开心那就没什么问题了；。

支持并行化，这个地方得说明一下，这可是xgboost的闪光点，啥是闪光点，就是直接的效果是训练速度快，boosting技术里下一步还要依赖前面树的训练加上预测，那树与树之间按理来说只能串行哪！大家琢磨琢磨，哪能并行！对，在选最佳分裂点，而后开始枚举的时候并行！（据说刚好这个也是树形成最费时间的阶段）注意啦：同层级节点能够并行。之于某个特定节点，于节点内部挑选最佳分裂点，针对候选分裂点计算增益借助多线程并行操作。—— 以较少的离散值当作分割点着实简便易行，好比依据“是否是单身”来分裂节点进而计算增益极为轻松容易，然而像“月收入”这般的特征，其取值数量众多，涵盖从5k至50k的范围，绝不可能针对每个分割点都去尝试一番来计算分裂增益吧？（举例而言，若月收入特征具备1000个取值，难道要将这1000个均作为分裂候选考虑进去？）。缺点一为计算量pg国际电子游戏app，缺点二是出现叶子节点样本过少，存在过拟合情况。我们通常习惯划分区间，如此一来问题便产生了，这个区间分割点究竟如何确定呢，难道是平均分割吗。作者采取了如下做法，其方法名字是Weighted Quantile Sketch。大家可还记得每个样本在节点，也就是那个将要分裂的节点处的loss function一阶导数gi，以及二阶差值 hi ，它们用于衡量预测值变化所带来的loss function变化。拿将样本“月收入”进行升序排列来说，有5k、5.2k、5.3k、…、52k，分割线分别是“收入1”、“收入2”、…、“收入j”，当满足每个间隔的样本的hi之和除以总样本的hi之和为某个百分比ϵ时，我这里说的是近似的表述方式，那么大约可以共分成1 / ϵ个分裂点 。

叉梯度提升树的第一直观感受是具备防止过度拟合作用以及各种支持分布式运用或者并行处理的特性，所以通常有这样地传言，这种厉害的工具成效良好，属于集成学习的高级配置，并且训练效率高，是因为其具备分布式特点，和深度学习相比较而言，对于样本数量以及特征数据类别需遵循的精确方式规定并没有这般严苛，其适用范畴较为广泛。叉梯度提升树与深度学习二者之间的关联，陈天奇在问答网站上做出了这样的解释，不同的机器学习模式适用于不同种类的任务。深度神经网络凭借对时间与空间位置构建模型，能够出色地捕捉图像、语音、文本等这类高维度数据 。然而，以可解释性、输入数据不变性、更易于调参等特性著称，这些特性正是某些深度神经网络所欠缺的，基于树模型的XGBoost却能够出色并且妥善地处理表格数据。