pg国际电子游戏app 二、GBDT小结

决策树算法，一种基于迭代构造的算法可知为GBDT（Gradient Boosting Decision Tree）它又能简便缩写成MART（Multiple Additive Regression Tree）或者GBRT（Gradient Boosting Regression Tree），虽然称法里既有Gradient，同时又存在Boosting，但其原理浅显易懂（固然详尽推导存在一点难度）。[id_[id_1539561729]64949414]

[id_8321[id_168274186]737]

今日要学的GBDT，同样是Boosting大家庭一员，自算法诞生起，它就和SVM一起，被视作泛化能力较强的算法，近些年来，更因被用于构建搜索排序的机器学习模型，而引发广泛关注。

[id_2[id_1937248999]1457]

那么，这般极为优秀的算法于实际当中究竟是怎样开展工作的呀？其背后的根本原理又是啥呢？接下来，我们就要踏入算法的内部，去揭开这把所谓“屠龙宝刀”的神秘的遮盖物呀。

一、GBDT之DT——回归树

广义线性模型主要是包含三个概念而构成的：回归决策树，梯度提升，以及收缩，只是将这三个概念搞清楚了，我们才能够理解算法的基本原理。首先进而学习第一个概念：回归决策树，也就是回归决策树。

说起决策树，不少人下意识会想到常见的、用于分类的决策树，像ID3、C4.5、CART等，然而要是把GBDT里的DT也当作分类决策树，那就完全错了。事实上，决策树不光能够被运用在分类方面，还能够被运用在回归方面，它的作用是进行数值预测，像明天的温度、用户的年龄之类的，并且对依据回归树所得出的数值做加减是具备意义的（好比10岁加上5岁再减去3岁等于12岁），这是有别于分类树的一个明显特点（毕竟男加上女等于到底是男是女呢，这样的运算根本没道理）。GBDT在运行之际便运用到了回归树的这个特性，它把累加所有树的结果当作最终的结果。所以，GBDT里的所有决策树都是回归树，并非分类树。

[id_108[id_1436210238]48234]

作为对比，简要回顾一下分类树的运行过程：以ID3作为例子，逐个穷举每一个属性特征的信息增益值，在每一次的时候，都去选取让信息增益最大的特征来进行分枝，一直到分类完成，或者达到预先设定的终止条件，进而实现决策树的递归构建。

回归树的运行流程与分类树基本类似，但有以下两点不同之处：

通常而言，回归树进行的分枝，不太容易达成每个叶子节点上的属性值都是唯一的情况，而是在于更多地抵达我们预先设定的终止条件就行（像是叶子个数的上限），如此一来必然会存在多个属性的取值，进而此节点处的预测值自然而然地就是基于这些样本所获取到的平均值了。

二、GBDT之GB——梯度提升

在对回归树有了初步的知晓之后，接着来瞧一瞧第二个概念问鼎赏金女王pg官网入口下载，那便是梯度提升（Gradient Boosting ）。，。

首当其冲要明晰，GB自身是一种理念，并非一个特定的算法，其基础思想是，顺着梯度方向，构建一连串的弱分类器函数，并且以某种权重组合在一起，进而形成用以最终决策的强分类器（鉴于梯度提升的具体情形与数学推导存在一定复杂性，而且即便不晓得这块知识的前因后果也不会妨碍对算法自身的理解，基于这样的考量，本文将不涉及“Gradient”，梯度提升的内容也会置于下一篇文章详细阐释）。

那这一系列的弱分类器究竟是怎样形成的呐？这便是GBDT的核心之处：每一棵树所学习的乃是之前所有树结论与的残差，这个残差是一个加预测值后能够得到真实值的累加量 。

说出一个简易的实例，同样是以年龄来开展分枝，假定我们 A 的实际年龄为 18 岁，然而第一棵树所预估的年龄乃是 12 岁，也就是残差为 6 岁。那么在第二棵树当中我们将 A 的年龄设定为 6 岁来展开学习，要是第二棵树确实能够把 A 划分到 6 岁的叶子节点，那把两棵树的结论加起来就是 A 的真实年龄；要是第二棵树的结论是 5 岁，那么 A 依旧存有 1 岁的残差，在第三棵树里 A 的年龄就变为 1 岁……按照这样的方式类推持续学习下去，这便是梯度提升在 GBDT 算法里的直观意义。

[id_420409586]

往后则是借助训练一个用以预测年龄的模型，来呈现算法的运作流程，（此节的内容以及图片引用自博客文章GBDT（MART）迭代决策树入门教程 | 简介） 。

首先，存在训练集，其中有四个人，分别是A、B、C、D，他们年龄各异，A的年龄是14，B的年龄是16，C的年龄是24，D的年龄是26。其中，A是高一学生，B是高三学生；C是应届毕业生，D是工作两年的员工。可用于分枝的特征包含上网时长、购物金额、上网所在时段以及对百度知道的使用方式等等。倘若运用一棵传统的回归决策树来进行训练，就会得到如下图所示的结果：

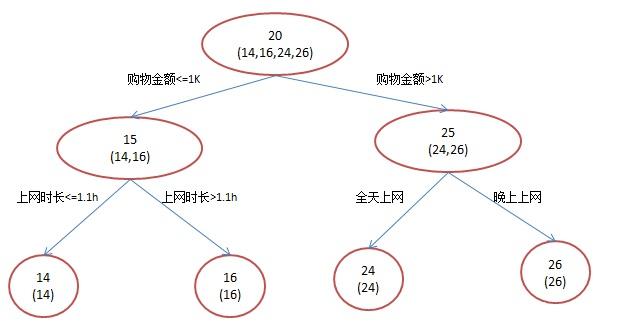
要是采用GBDT去做这件事情，鉴于数据量过少，我们规定叶子节点最多存在两个，也就是每一棵树唯有孤单一枝，尚且规定仅能学习两棵树，这般就会得出如同下图呈现的结果：

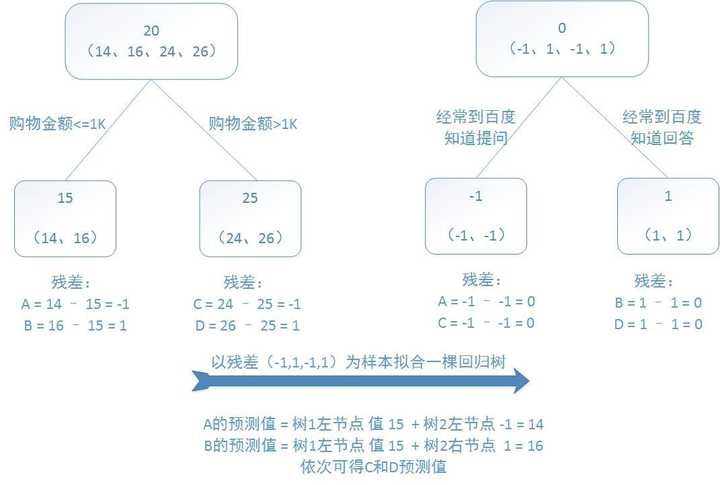
第一棵树的分枝情况和之前时相同，同样是运用购物金额来做区分的，有两拨人，他们各自将年龄均值当作预测值，进而得到了残差值，分别是 -1、1、-1、1，之后用这些残差值去替换初始值，以此来训练生成第二棵回归树，要是新的预测值和残差是相等的，那么只要把第二棵树的结论累加到第一棵树上，这样就能够得到真实年龄了。

第二个棵树仅仅存有俩值，分别是1以及-1，径直能够划分成俩节点。在这个时候，所有人身上的残差均为0，也就是说，每一个人所获得的皆是真实的预测数值。

将两棵回归树预测结果进行汇总，解释如下：

将初始的回归树跟生成了 的那能够把最终结果呈现同一状态并且相同的GBDT，予以两相比较，如果会发现那样的情况，那么我们究竟是基于何种具备怎样理由进行为何要还用到并且使用GBDT呢这般操作呢？ 。

答案是针对模型过拟合的思索，过拟合指的是，旨在达成训练集精度的提升，从而掌握了诸多“仅于训练集范畴之内才得以成立的规律”，致使在更换数据集之后，当下规律所呈现的预测精度难以令人感到满意，毕竟，于训练精度以及实际精度（或者测试精度）之间，后者才是我们切实想获取到的 。

在上述例子当中，最初的回归树，为了达成百分之百精度，运用了三个特征，分别是上网时长、时段、网购金额，然而经过观察能够发现，分枝“上网时长>1.1h”明显出现了过拟合的情况，不能排除恰巧A上网时长为1.5h，B上网时长为1小时，所以凭借上网时间是否大于1.1小时去判别所有人的年龄，显然是违背常识的。

在GBDT当中，有两棵回归树，它们只用了两个特征，这两个特征是购物金额与对百度知道的使用方式，借助这两个特征就达成了100%的预测精度。其分枝依据相较于上网时长特征，更加合乎逻辑。并且算法在运行的时候，体现出了“如无必要，勿增实体”的奥卡姆剃刀原理。

四、GBDT的第三个基本概念为Shrinkage（缩减） “缩减” 在中文里是其含义 它基本思想所表达的乃是：比起每次迈一大步很快就逼近其结果的行事方式，每次仅迈一小步逐步靠近那结果之情况反倒愈发利于将逾矩拟合规避。若换种说法来讲，那缩减之思想并非全然信赖每一棵的残差树，它觉得每一颗树仅仅学到了真理的一小部分，在开展累加操作时仅累加一小部分；只能够借助多学习几棵数据树才可以使不足得以弥补 。

收缩仍然是以残差当成学习目标，然而因为它采用的是逐步朝着目标逼近的方式，致使各个树的残差是逐渐变化的而非急剧变化的。之所以会这样去做也是基于对模型过拟合的思索（更为详尽的内容能够参考文末所给出的参考资料）。

GBDT的基本内容差不多介绍完了，在接下来的文章里，我们会从梯度这个方面对算法展开推导以及学习。

一、GBDT的梯度提升过程

在前面的那一篇文章当中，我们针对GBDT算法的基本概念进行了细致入微的讲述，并且借助一个简易的小例子，对它于实际进行运用时的运行流程予以了阐述，能够说我们针对该算法已然具备了一个大概的认识。然而，还存在着一个问题有待去解决，那便是怎么去领会GBDT里的Gradient（梯度）呢？

一众皆知，以Boosting为根基的集成学习，是借由迭代获取一连串的弱学习器，接着凭借各异的组合策略得出相应的强学习器。在GBDT的迭代进程里，假定前一轮所获的强学习器为 。

，对应的损失函数则为

。因此新一轮迭代的目的就是找到一个弱学习器

[id_627501006]

达到最小。

那么问题的关键之处便在于对于损失函数的度量，而这恰又正是难点的所在之处，毕竟损失函数存在各式各样的状况，要找寻到一种通用的拟合办法究竟该如何去做呢？

在上图之中，呈现的乃是常用的损失函数以及 其梯度 ，该图片的来源是（The Elements of Statistical Learning），下文与此相同 ，句号 。 （修改后的句子在按照要求拆分后更符合中文理解习惯，但仍保留符合场景不太好理解的表达）。

对这一问题而言之话讲，机器学习领域里的厉害人物Freidman推出了梯度提升算法呀：凭借那如同如雷贯耳般的最速下降的近似手段法子呀pg问鼎安卓下载，亦是要借助损失函数的负梯度于当下模型所拥有的值呀，以此作为回归问题里提升树算法之内残差的近似数值呀，去拟合一棵回归树呢。

这样的话，第

轮的第

个样本的负梯度表示为：

，算法的完整流程如下：

接下来对上图中的算法步骤进行详细解释：

二、GBDT小结

到此为止，GBDT的相关内容已差不多讲完了，对于这个算法而言，有两个方面，一方面，我们能够从残差的视角进行理解，此说法是指，每一棵回归树都是在学习先前树的残差；另一方面，我们也能够从梯度的角度去掌握该算法，也就是说，每一棵回归树是借助梯度下降法来学习之前树的梯度下降值。

从这样看的情况来说，这两种理解的角度，在总体流程这个方面，以及输入输出这个方面，是没有区别的，它们都是属于迭代回归树。它们都是通过累加每一棵数的结果，以此作为最终的结果。每一棵数都在进行学习，针对前面数所还存在的不足。然而呢，不同的地方就在于，每一步进行迭代之时，求解的方法是不一样的，前者运用残差，这里的残差是全局最优值，后者运用梯度，这里的梯度是局部最优方向。简单一点儿来表述就是，前者每一步在尝试朝着最终结果的方向去进行优化，而后者每一步则是尝试让当前的结果变得更好一点儿。

前者给人的观感相对更具科学性，毕竟存在绝对最优方向却不去借鉴，为何要舍易而难，偏离近在眼前的最优方向，执意去估量局部最优方向呢。其缘由根源于灵活性。前者最为明显突出的局限性则是，当它依赖残差状况时，损失函数通常被常规性地设定为用以反映残差的均方差形式，所以在应对纯回归问题以外的其他问题时，面临着重重困难。而后者所采用的求解方式是梯度下降法，只要但凡属于可求导性状的损失函数，都能够得以运用。

最后小结一下GBDT算法的优缺点。

优点：

缺点：

三、GBDT算法的R实现

在R这个环境里，我们能够借助gbm包当中的有关函数把算法给实现出来，第一步要做的是进行安装，之后还要进行载入，明白了吧。

> install.packages([id_1110565834])
> library(gbm)

# gbm()函数的调用公式及主要参数如下：
> gbm(formula = formula(data),distribution = "bernoulli",data = list(),
+ n.trees = 100,shrinkage = 0.001,...,
+ bag.fraction = [id_1018652419],interaction.depth = 1)
损失函数的形式有多种可选择，其中有“gaussian”（即平方误差），还有“laplace”（绝对损失），也有“bernoulli”（用于0 - 1结果的逻辑回归），另外还有“huberized”（用于0 - 1结果的huberized铰链损失）等等。
# n.trees:迭代次数
关于shrinkage也就是学习速率，我们大家都明确知晓，步子要是迈得过大轻易就会扯着蛋，因而学习速率越小越好，可是步子倘若太小，那么步数就必须增加，这意味着训练的迭代次数需要加大才能够让模型达到最优，如此训练所需的时间以及计算资源也会相应地加大了，gbm的作者所采用的经验法则是将参数设置在0.01至0.001之间 。
# bag.fraction:再抽样比率
# 除此之外,函数中还有其他参数,可自行查阅相关文档

接下去选用TH.data包当中的bodyfat数据集来开展实证分析，此数据集记载了71名健康女性的身体 datum，涵盖年龄、腰围、臀围等变量，用以对于身体脂肪（DEXfat）的预测剖析。

> library(TH.data)
> data(bodyfat)
> dim(bodyfat)
[1] 71 10
> head(bodyfat)
47  57  41.68     100.0   112.0          7.1         9.4     4.42     4.95 
48  65  43.29      99.5   116.5          6.5         8.9     4.63     5.01 
49  59  35.41      96.0   108.5          [id_1330054763]         8.9     4.12     4.74     
50  58  22.79      72.0    96.5          6.1         9.2     4.03     4.48     
51  60  36.42      89.5   100.5          7.1        10.0     4.24     4.68     
52  61  24.13      83.5    97.0          6.5         8.8     3.55     [id_1611654606]       
   anthro3c anthro4
47     4.50    6.13
48     4.48    6.37
49     4.60    5.82
50     [id_1369486852]    5.66
51     4.15    5.91
52     3.64    5.14 

# 模型构建
> gbdt_model <- gbm(DEXfat[id_1458453390].,distribution = 'gaussian',data=bodyfat,
+ n.trees=1000,shrinkage = 0.01)

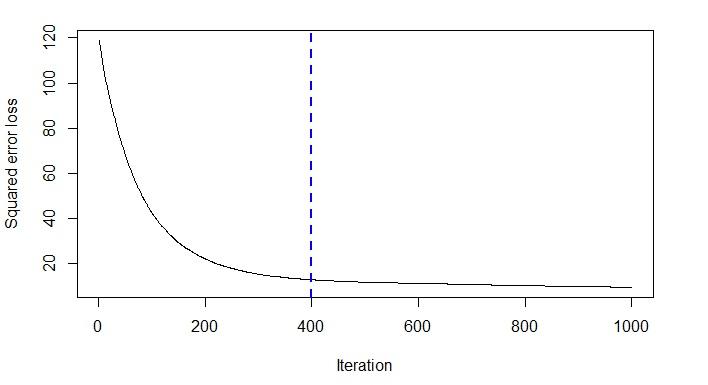
# 使用gbm.pref()确定最佳迭代次数
> best.iter <- gbm.perf(gbdt_model)
> best.iter
[1] 399

# 查看各变量的重要程度
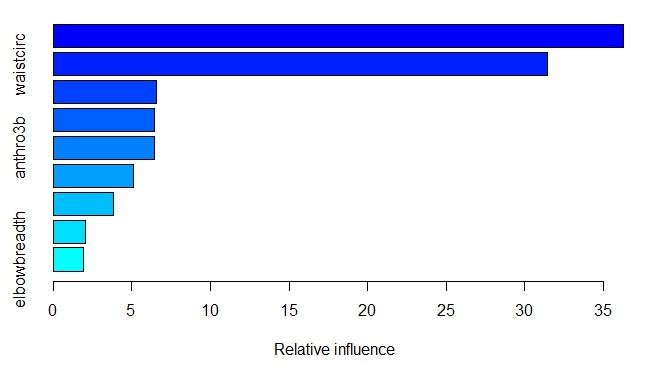
> summary.gbm(gbdt_model,best.iter)
                      var   rel.inf
hipcirc           hipcirc 36.276643
waistcirc       waistcirc 31.447718
anthro3c         anthro3c  6.561716
[id_127216312]6.447923
anthro3b         anthro3b  6.423434
[id_1496489458]5.068798
kneebreadth   kneebreadth  3.834679
age                   age  2.050727
elbowbreadth elbowbreadth  1.888361

# 查看各变量的边际效应,用数值来自定义变量查询
> par(mfrow=c(1,3))
> plot.gbm(gbdt_model,3,best.iter)
> plot.gbm(gbdt_model,4,best.iter)
> plot.gbm(gbdt_model,5,best.iter)

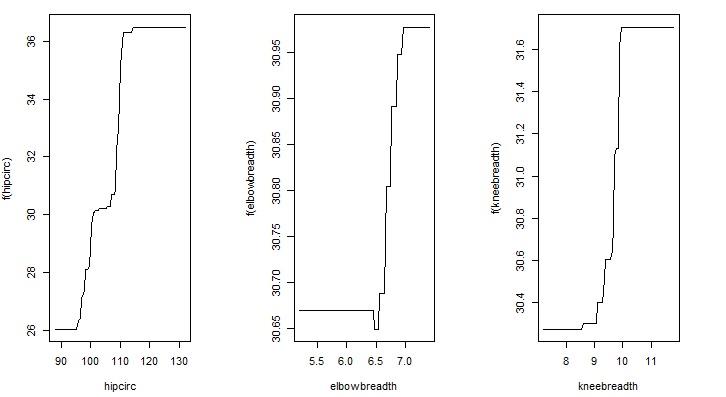
# 使用建立好的模型进行DEXfat值的预测
> gbdt_fit <- predict(gbdt_model,bodyfat,best.iter)
> head(gbdt_fit)
[1] 43.78154 43.51006 36.23172 23.54703 36.71636 22.47789
# 计算预测结果与真实结果的方差值
> print(sum((bodyfat$DEXfat-gbdt_fit)^2))
[1] 924.0749

如下是GBDT算法于R里的一个实例运用，鉴于我们的目标是获取所需的预测数值，因而没办法靠着对比预测的值跟实际的值的相符程度（也就是预测的精准度）去判定模型的好与坏，转而选用了方差当作衡量模型好坏的标准。要是我们想着查看一个模型在新的数据集之上的表现状况怎样，能够考虑生成训练的数据集，以及测试的数据集，操作步骤如下：

> index <- sample(2,nrow(bodyfat),replace = TRUE,prob=c(0.7,0.3))
> traindata <- bodyfat[index==1,]
> testdata <- bodyfat[index==2,]

采用这样的情形，生成模型会选用traindata，而进行预估的时候可选用testdata。

最后的需留意之处是，于bodyfat这个案例内，我们最初选用了回归里极其常见的平方损失，可是要晓得彼此存在差异的损失函数对于最终的预测精准程度会产生各不相同的作用，其他参数也是如此这般。故而，要是打算对模型予以进一步的改良，在参数挑选这儿还是有着诸多可探究之处的。

一、XGBoost简介

于GBDT的学习进程里头，众多博客都提及了此算法的升级版即XGBoost，同时针对它赞誉极高。故而，这部分知识，涵盖算法基础内容，及数学推导与案例实现，会借两篇文章篇幅去达成学习掌握。

凭借之前的学习，我们已然清楚，GBDT是一种基于集成理念的Boosting学习器，它运用梯度提升的方式来开展每一轮的迭代，进而最终构建出强学习器，如此一来，算法的运行常常要生成一定数目的树方可达成让我们感到满意的准确率。要是数据集规模大且较为繁杂的时候，运行一回极有可能得进行几千次的迭代运算，这会给我们运用算法带来极大的计算瓶颈。

问题针对这一，华盛顿大学的陈天奇博士开发出了XGBoost（eXtreme Gradient Boosting），它有着Gradient Boosting Machine的 一个c++实现，并且在原有的基础之上加以改进，进而极大地提升了模型训练速度以及预测精度。能够这么讲，XGBoost是Gradient Boosting的高效实现。

XGBoost最为突出的特点是，它能够自行借助CPU的多线程来开展并行计算，与此同时，于算法层面予以改进从而提升了精度。在Kaggle的希格斯子信号识别竞赛里，XGBoost凭借出众的效率以及较高的预测准确度，在比赛论坛中引发了参赛选手的广泛关注，在1700多支队伍的激烈角逐中占据了一席之地。伴随其在Kaggle社区知名度的提升免费qq黄钻网站大全下载，在其他比赛中也有队伍借助XGBoost荣获第一。

接下来学习XGBoost算法的数学推导过程。

二、目标函数：损失与正则

在监督学习里，我们常常进行构造一个目标函数，以及构造一个预测函数的操作，运用训练样本针对目标函数实施最小化，进而学习得出相关的参数，接着借助预测函数以及由训练样本所得到的参数，来针对未知的样本开展分类的标注或者数值的预测。在XGBoost这一范畴中，目标函数呈现出这样的形式：

正则化项，引入它是有原因的，我们期望生成的模型能够精准地预测新的样本，也就是应用于测试数据集这部分，而不是单纯地去拟合训练集的结果，因为那样会引发过拟合情况。所以要在确保模型“简单”的状况下，致力于最小化训练误差，如此得到的参数才具备良好的泛化性能。而正则项的作用就是惩罚复杂的模型，防止预测模型过度拟合训练数据，常用的正则包括 。

正则与

正则。

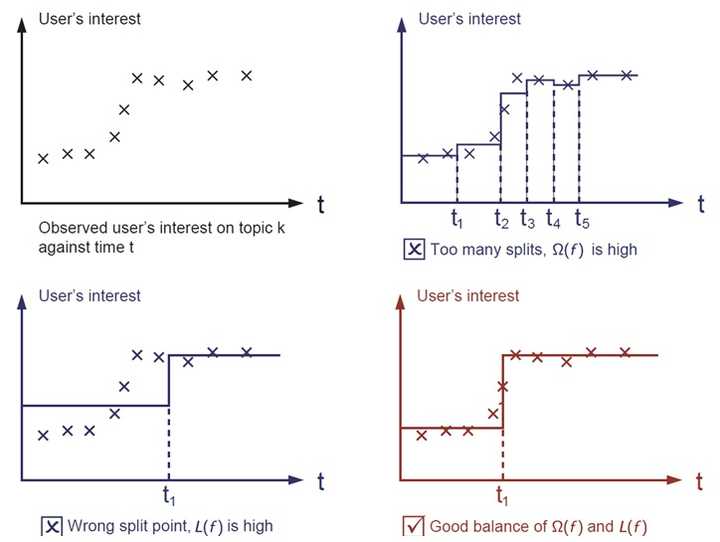
图片所呈现出来的，便是损失函数跟正则化项于模型里的运用情况（图片出处：Introduction to Boosted Trees）。经观察发觉，要是目标函数当中，损失函数的权重处于过高状态，那么模型的预测精准度就不太能让人满意，相反要是正则项的权重过高，那所生成的模型就会遭遇过拟合情形，极难针对新的数据集给出有效的预测结果。唯有将两者之间的关系平衡精妙得当，成功准确操控好模型复杂度，且于这个根基之上对参数展开求解，如此这般生成的模型，才能够达成所谓的“简单有效”（而这其实就是机器学习范畴里的偏差方差均衡）。

三、XGBoost的推导过程

1. 目标函数的迭代与泰勒展开

鉴于先前已然学习过树的生成及集成方式，在此处便不再进行详细叙述。首先，我们能够将某一回迭代之后集成的那个模型表述成这样子：

也就是上文中的

相对应的目标函数：

将这两个公式进行扩展，应用在前

轮的模型迭代中，具体表示为：

就是前

轮的模型预测，

为新

轮加入的预测函数。

这里自然就涉及一个问题：如何选择在每一轮中加入的

呢？答案很直接，选取的

我们要让目标函数尽可能最大限度地减小，这里运用了Boosting的基本理念，也就是当前的基学习器着重关注以往所有学习器出错的那些数据样本，通过这样的方式来达成提升的成效。首先得对目标函数进行改写，呈现如下：

如果我们考虑使用平方误差作为损失函数，公式可改写为：

在更为普遍的情形下，针对并非平方误差的状况而言，我们能够运用如下这般的泰勒展开近似办法，以此来界定一个近似的目标函数，进而便于我们开展这一步骤的计算。

泰勒展开：

其中

要是把常数项除去，我们就会发觉，这个目标函数具备一个极其显著的特性，它单单依傍于每个数据点在误差函数方面的一阶导数，还依傍于二阶导数。

这是括号。有一些人有可能会进行询问，这个公式好像相较于我们以前所学习的决策树学习而言更难以理解。到底为啥要耗费如此多的精力去做推导呢 ？

这是由于，这般去做会致使我们能够较为清晰明确地领悟整体目标究竟是什么。并且，能够一步步地推导出怎样开展树的学习。 这一抽象形态对于达成机器学习工具而言也是颇具助益的。 因为它涵盖了所有能够求导的目标函数。亦即，有了此形式，我们所撰写的代码能够用以求解涵盖回归、分类以及排序的各类问题。正式的推导能够让机器学习的工具更为普遍化 。

2. 决策树的复杂度

接着来讨论如何定义树的复杂度。我们先对于

的定义做一下细化，把树拆分成结构部分

和叶子权重部分

。其中结构函数

把输入映射到叶子的索引号上面去，而

给定了每个索引号对应的叶子分数是什么。具体公式为：

当我们给定上述定义后，那么一棵树的复杂度就为

这种复杂度涵盖了一棵树木之中节点的数量（位于左侧），及单独每个树叶节点之上那些输出分数的。

模平方，位于右侧。当然，这并非是唯一的一种给予定义的方式，然而，通过这一定义方式所学习得出的树，其效果通常而言都相对比较良好。

简单提及一下

两个系数的作用，

设其为作为叶子节点的系数，且该系数让XGBoost展开，在优化目标函数之际，与此同时，其相当于做了预剪枝，最终呈现如此状态 。

作为

平方模的系数也是要起到防止过拟合的作用。

这里列举一个小小的例子，便于加深对于复杂度的理解，（图片的来源是：Introduction to Boosted Trees，下同）。

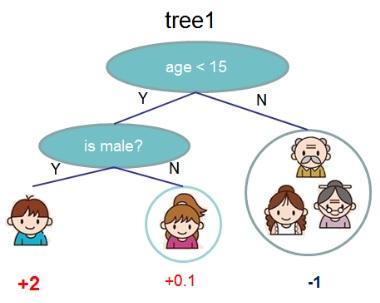
所示的图呈现出的是实际所生成的一棵决策树，位于底部的数字乃是用来代表决策树的预测值，如此一来，这棵树的复杂度自然而然地的也就为：

3. 目标函数的最小化

随后便是极其关键的一步，于这般新颖的定义范畴内，我们能够将目标函数予以如下的改写，当中 ，。

被定义为每个叶子上面样本集合

分别定义

，上式简化为

由这个情况，我们把目标函数转变成为一个针对一元二次方程来求取最小值的问题，且限定在此式之中，变量便是。

，函数本质上是关于

的二次函数），略去求解步骤，最终结果如下所示：

乍一看目标函数的计算与树的结构函数

没存在啥关联，然而要是我们认真回溯目标函数的组成情况，就会发觉当中 。

的取值都是由第

个树叶上数据样本所决定的。而第

个树叶上所具有的数据样本则是由树结构函数

决定的。也就是说，一旦树的结构

能够确定，那么依据上式就可以把相应的目标函数计算出来。那么树的生成问题也就转变成要找到一个最优的树结构 ， 。

，使得它具有最小的目标函数。

计算求得的

在指定一个树的结构之际，目标函数所能减少的最大量是多少。因而我们能够将其称作结构分数(structure score) 。

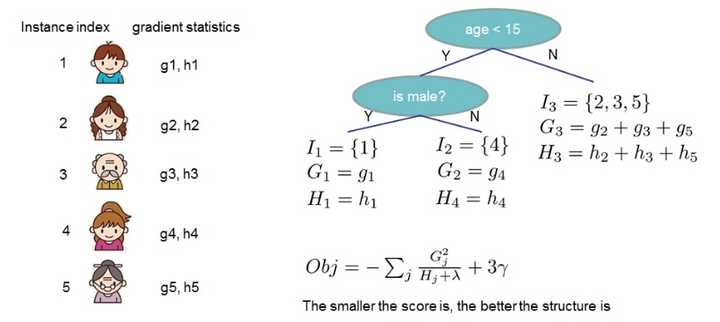
上边所呈现的是结构分数的一回实际运用情况，依据决策树的预测成果得出各个样本的梯度数据，随后计算出实际的结构分数。正如图里所说的那样，分数越小，意味着树的结构越优良。

4. 枚举树的结构——贪心法

在前面所做分析的基础之上，当寻觅到最优的树结构之际，我们能够持续地列举各类不同树的结构，借助这个打分函数去探寻出一个具备最优结构的树，将其添加至我们的模型当中，随后再度重复这样的操作。然而，列举所有树结构这一操作并非切实可行，在此处XGBoost运用了常用的贪心法，也就是每一回尝试针对已有的叶子添加一个分割。对于某一个具体的分割方案，我们能够获取的增益可经由如下公式计算得出：

其中

代表左子树分数，

代表右子树分数，

代表不分割时我们可以获得的分数，

代表加入新叶子节点引入的复杂度代价。

每次进行扩展的时候，我们依旧得去把所有有可能存在的分割方案给列举出来，那么要怎样才能够以高效的方式去列举所有的分割呢？假定是需要列举全部。

这样的条件，那么对于某个特定的分割

我们要计算

左边和右边的导数和，在实际应用中如下图所示：

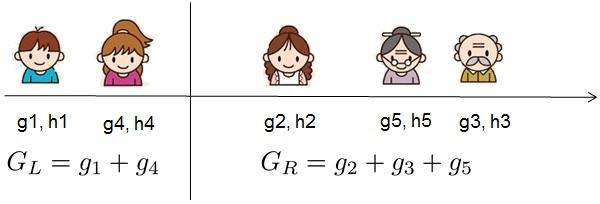
我们可以发现对于所有的

，我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度与

。然后用上面的公式计算每个分割方案的分数就可以了。

但要留意的是，引入的分割不见得会让情况朝着好的方向发展，这是由于在引入分割的那会儿，也把针对新叶子的惩罚项给引入了。所以一般来讲，得设定一个阈值，要是引入的分割所带来的增益比一个阀值小的时候，我们能够把这个分割给剔除掉。另外，在XGBoost的实际操作过程中，常常会设定树的深度，以此来把控树的复杂度，防止单个树过于繁杂而引发过拟合问题。

到这个地方截止，XGBoost的数学方面的推导就简单扼要地介绍完了。在接下来的一篇文章当中，我们将会去知晓该算法相较于GBDT的出色特性以及学习XGBoost的R语言实现。

这边所讲的这个文本内容呢，是关于GBDT算法著作里的第四个篇章，之前已然完成了XGBoost这一算法基础性质等事项的介绍以及与之相关联的数学推导过程，在这之后呢，即将开启对于XGBoost有别于GBDT的那些独有的特性方面的学习，还有针对该算法的R语言实现方式的学习。一、XGBoost具备的优良特性 。

同样属于梯度提升，同样身为集成学习，那么XGBoost相较于GBDT究竟好在哪些方面呢？结合前面的推导进程以及相关博客文章（参考资料在文末），大致能够总结成以下几点：

二、xgboost包安装与数据准备

在R中，xgboost包用于算法的实现，首先进行安装

xgb oost包进行安装之际，要将R升级到3点3点0以上的版本，不然安装时不会成功，。
> install.packages('xgboost')
# 也可使用devtools包安装github版本
> devtools::install_github('dmlc/xgboost', subdir='R-package')
> library(xgboost)

在包里面，存在着一组蘑菇数据集， 是能够去供人使用的，我们所设置达成的目标呢，是要对蘑菇能不能够用作食用，这个（属于）分类任务进行预测， 这一组数据集，已经被划分而成了训练数据，还有测试数据 。

> data(agaricus.train, package='xgboost')
> data(agaricus.test, package='xgboost')
> train <- agaricus.train 
> test <- agaricus.test

# 整个数据集是由data和label组成的list
> class(train)
[1] "list"
# 查看数据维度
> dim(train$data)
[1] 6513  126
> dim(test$data)
[1] 1611  126

在此数据集中，data属于dgCMatrix类的稀疏矩阵，label是数值型向量，其由{0,1}所构成。
> str(train)
List of 2
 $ data :Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
  .. ..@ i       : int [1:143286] 2 6 8 11 18 20 21 24 28 32 ...
  .. ..@ p       : int [1:127] 0 369 372 3306 5845 6489 6513 8380 8384 10991 ...
  .. ..@ Dim     : int [1:2] 6513 126
  .. ..@ Dimnames:List of 2
  .. .. ..$ : NULL
  .. .. ..$ : chr [1:126] "cap-shape=bell" "cap-shape=conical" "cap-shape=convex" "cap-shape=flat" ...
  .. ..@ x       : num [1:143286] 1 1 1 1 1 1 1 1 1 1 ...
  .. ..@ factors : list()
 $ label: num [1:6513] 1 0 0 1 0 0 0 1 0 0 ...

三、构建模型和预测实现

xgboost包给出了两个函数用以模型构建，这两个函数分别是xgboost()和xgb.train()，其中，前者能够满足对于算法参数的大致条件设定，而后者呢，在前者的基础之上能够达成一些更为高级的功能，并以此作为前提条件 。

# data与label分别指定数据与标签
树的深度是max.deph，其默认值是6，在这个数据集中分类问题相当简单，将其设置为2就行 。
# nthread：并行运算的CPU的线程数,设置为2;
# nround：生成树的棵数
# objective 设成 "binary:logistic" 的用处 在于去设置 逻辑回归二分类模型 punctuation。
> xgboost_model <- xgboost(data = train$data, label = train$label, max.depth = 2, eta = 1, nthread = 2, nround = 2, objective = "binary:logistic")
# 得到两次迭代的训练误差
[1]	train-error:0.046522 
[2]	train-error:0.022263 

xgboost函数能够调用的参数数目颇多，在这里就不进行详尽展示说明了，能够参考博客文章快速上手：于R里运用XGBoost算法之中的“在xgboost里运用参数”这一节，该文章把这些参数划分成为通用、辅助以及任务参数这三大类别，对于我们把控算法以及调整参数有着极大的助力。

# 设置verbose参数,可以显示内部的学习过程
> xgboost_model <- xgboost(data = train$data, label = train$label, 
+ max.depth = 2, eta = 1, nthread = 2, nround = 2, verbose = 2,
+ objective = "binary:logistic")
[13:56:36] amalgamation/../src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 6 extra nodes, 0 pruned nodes, max_depth=2
[1]	train-error:0.046522 
[13:56:36] amalgamation/../src/tree/updater_prune.cc:74: tree pruning end, 1 roots, 4 extra nodes, 0 pruned nodes, max_depth=2
[2]	train-error:0.022263

# 将建立好的模型用于预测新的数据集
> xgboost_pred <- predict(xgboost_model, test$data)
> head(xgboost_pred)
[1] 0.28583017 0.92392391 0.28583017 0.28583017 0.05169873 0.92392391
已给定的，是每一单样本的预测概率之值，经进一步转化后，能够获取具体的预测分类 。
> prediction <- as.numeric(xgboost_pred > 0.5)
> head(prediction)
[1] 0 1 0 0 0 1
> model_accuracy <- table(prediction,test$label)
> model_accuracy
          
prediction   0   1
         0 813  13
         1  22 763
> model_accuracy_1 <- sum(diag(model_accuracy))/sum(model_accuracy)
> model_accuracy_1
[1] 0.9782744

四、XGBoost的高级功能

xgb.train()函数能够达成某些高级功效，可以用以协助我们朝着前行的方向对模型予以更进一步的优化处理。

要使用函数，之前得把数据集转一番哦，把它变换成xgb.Dmatrix这种格式嘞。
> dtrain <- xgb.DMatrix(data = train$data, label=train$label)
> dtest <- xgb.DMatrix(data = test$data, label=test$label)

采用watchlist参数，能够一并获取训练数据的误差，以及测试数据的误差 。
> watchlist <- list(train=dtrain, test=dtest)
> xgboost_model <- xgb.train(data=dtrain, max.depth=2, eta=1, nthread = 2,
+ nround = 3,objective = "binary:logistic",watchlist = watchlist)
[1]	train-error:0.046522	test-error:0.042831 
[2]	train-error:0.022263	test-error:0.021726
[3]	train-error:0.007063	test-error:0.006207

# 自定义损失函数,可同时观察两种损失函数的表现
该参数可用于评估指标的参数涵盖了，诸如“logloss”的这一类型，还有“error”类别，以及“rmse”这种种类等等 。
> xgboost_model <- xgb.train(data=dtrain, max.depth=2, eta=1, nthread = 2,
+ nround=3, watchlist=watchlist, eval.metric = "error", 
+ eval.metric = "logloss", objective = "binary:logistic")
[1]	train-error:0.046522	train-logloss:0.233376	test-error:0.042831	test-logloss:0.226686 
[2]	train-error:0.022263	train-logloss:0.136658	test-error:0.021726	test-logloss:0.137874 
[3]	train-error:0.007063	train-logloss:0.082531	test-error:0.006207	test-logloss:0.080461

# 查看特征的重要性,方便我们在模型优化时进行特征筛选
> importance_matrix <- xgb.importance(model = xgboost_model)
> importance_matrix
特征，增益，覆盖范围，频率 ，这几个词分别代表着不同的含义 ，特征体现了事物独有的特点与特性 ，增益表示着增加、提升的程度 ，。
1:      28 0.60036585 0.41841659     0.250
2:      55 0.15214681 0.16140352     0.125
3:      59 0.10936624 0.13772146     0.125
4:     101 0.04843973 0.07979724     0.125
5:     110 0.03391602 0.04120512     0.125
6:      66 0.02973248 0.03859211     0.125
7:     108 0.02603288 0.12286396     0.125
借助xgb.plot.importance()函数，去开展可视化呈现，。
> xgb.plot.importance(importance_matrix)

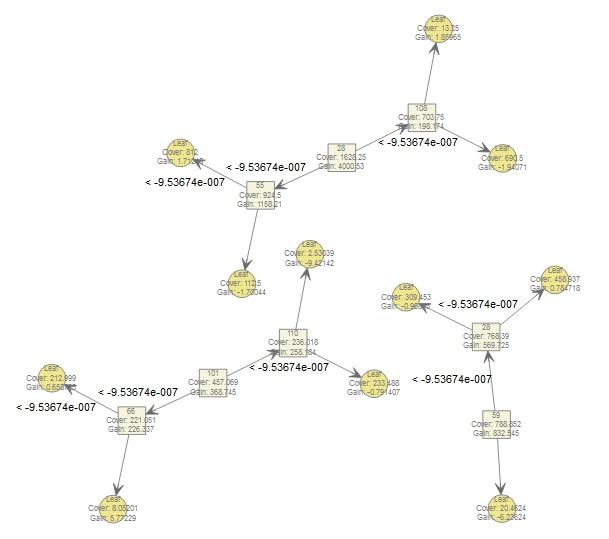
# 使用xgb.dump()查看模型的树结构
> xgb.dump(xgboost_model,with_stats = T)
 [1] "booster[0]"                                                            
 [2] "0:[f28<-9.53674e-007] yes=1,no=2,missing=1,gain=4000.53,cover=1628.25" 
 [3] "1:[f55<-9.53674e-007] yes=3,no=4,missing=3,gain=1158.21,cover=924.5"   
 [4] "3:leaf=0.513653,cover=812"                                             
 [5] 4，叶子的值是负零点五一零一三二，覆盖值一百一十二点五，。                                          
 [6] "2:[f108<-9.53674e-007] yes=5,no=6,missing=5,gain=198.174,cover=703.75" 
 [7] 5 ，其中 leaf 的值是等于负的 0.582213的 。cover 的值是 69。                                          
 [8] "6:leaf=0.557895,cover=13.25"
 ---
# 将上述结果通过树形结构图表达出来 
> xgb.plot.tree(model = xgboost_model)

此刻，XGBoost算法以及其R实现就只是简略介绍到这般地步了。尽管好像讲了不少内容，然而我们所掌握的不过是些非常浅显的东西罢了，不管是XGBoost自身具备的出色性能、借助繁杂的调参来实现对不同任务的支持，还是在实际运用中的具备高精度的预测，这些优势都意味着XGBoost算法有着极大的潜力空间，值得我们持续不断地去进行探索。